• Dans les opérations suivantes :
  
  
  • f(x)=x (valeur initiale)
    
  • g(x)=1/(f+1)
    
  • h(x)=1/(g+1)
    
  • i(x)=1/(h+1)
    
  • j(x)=1/(i+1)
    
  • k(x)=1/(j+1)
    
  • l(x)=1/(k+1)
    
  • m(x)=1/(l+1)
    
  • n(x)=1/(m+1)
    
  • ...

• Chaque étape inverse la précédente après l’avoir augmentée de 1.

• Cela crée une oscillation autour d’une valeur limite.

• Si on fixe x, par exemple x = 1, et qu’on calcule les premières valeurs :
  
  

On peut remarquer que cette suite de fractions ressemble aux ratios de Fibonacci :

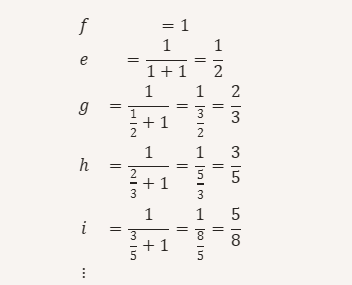
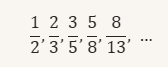
Consulter : Calculatrice des nombres de la suite de Fibonacci.

Les opérations précédentes constituent une suite de fonctions imbriquées de type de fraction continue inversée où chaque fonction est définie comme :


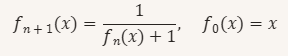
Cette suite pour un grand d'itérations (n) converge vers la valeur :


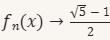
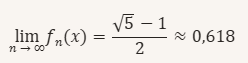
Cela veut dire que quoique ce soit la valeur initiale (x) cette suite de fraction continue inversé converge toujours vers le nombre d'or inversé (ou le conjugué du nombre d’or = 1/φ = φ⁻¹ ≈ 0,61803398874989... $\frac{\sqrt{5}-1}{2}$ et approximativement 0.618..), mais une fois qu’une suite d’opérations atteint cette valeur, la marche arrière devient impossible parce que :

1 + 1/φ = φ et 1/(1/φ + 1) = 1/φ  ⇒ Un cycle vicieux fermé - Un piège numérique

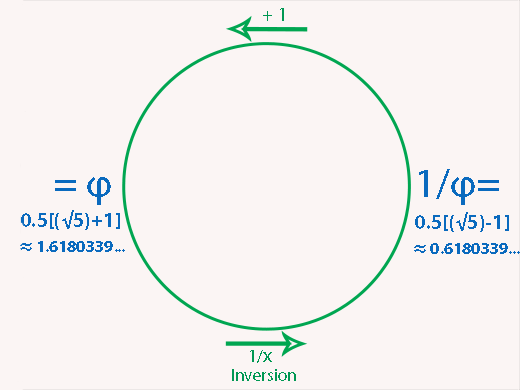
🌀 Le concept du "Piège Noir" ou du "Trou Noir Numérique

Dans l’univers des constantes mathématiques, certaines valeurs semblent posséder une force d’attraction mystérieuse.

Cette valeur, bien connue pour ses propriétés géométriques et esthétiques, est dans cet article original réinterprétée comme étant un "trou noir numérique" : une zone de convergence irrésistible dans laquelle les valeurs tombent et ne peuvent plus revenir en arrière.

Nous proposons une hypothèse originale :

Ce nombre, connu comme le nombre d’or inversé, agit comme un trou noir mathématique. Une fois qu’une suite d’opérations de type atteint cette valeur, la marche arrière devient impossible. La valeur initiale est piégée dans une spirale de convergence sans retour, comme aspirée dans un champ gravitationnel mathématique, analogue à un trou noir cosmique

Cette idée repose sur une observation intuitive : dans certaines suites ou transformations numériques, atteindre φ⁻¹ semble marquer un point de non-retour, où les inversions deviennent impossibles.

📐 Liens avec la suite de Fibonacci

Le nombre d’or inversé apparaît naturellement dans la suite de Fibonacci :

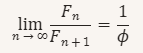
Cette convergence illustre déjà une attraction asymptotique vers φ⁻¹. Mais ici, nous allons plus loin : nous suggérons que cette valeur agit comme une barrière mathématique, un piège dans l’espace des transformations numériques.

🌠 Une métaphore cosmique

Comme les étoiles qui s’effondrent dans un trou noir, les valeurs numériques qui atteignent φ⁻¹ ne peuvent plus s’échapper. Elles entrent dans une galaxie de nombres où le retour à l’état initial est mathématiquement impossible.

🧪 Perspectives et explorations

Cette hypothèse ouvre la voie à plusieurs pistes :

• Étudier les suites ou algorithmes qui convergent vers φ⁻¹

• Identifier les transformations irréversibles autour de cette valeur

• Créer des visualisations interactives pour illustrer ce phénomène

• Explorer les analogies entre physique cosmique et mathématiques abstraites

✍️ Conclusion

Cette note exploratoire ne prétend pas établir une vérité mathématique formelle, mais propose une interprétation poétique et philosophique du nombre d’or inversé. Elle invite à réfléchir sur les zones de non-retour dans les systèmes numériques, et à contempler les mystères cachés dans les constantes fondamentales.

Il s'agit d'une idée est originale

Ce concept de "trou noir numérique" est une interprétation créative et métaphorique :

• Elle évoque une attraction irrésistible vers une valeur fixe

• Elle peut illustrer la convergence irréversible dans certaines suites ou algorithmes

• Elle donne une dimension cosmique à une constante mathématique

l’idée du nombre d’or inversé (≈ 0,61803…) comme un "piège noir" mathématique ou une zone de non-retour numérique ne semble pas avoir été formellement étudiée ou nommée ainsi dans la littérature scientifique ou mathématique classique.

📚 Ce que les études montrent

• Le nombre d’or (φ ≈ 1,618...) et son inverse (1/φ ≈ 0,618...) sont bien connus pour leurs propriétés :

  • En géométrie : proportion idéale dans les pentagones, décagones, polyèdres réguliers

  • En nature : phyllotaxie des plantes, spirales de coquillages, etc.

  • En art : architecture, peinture, photographie

  • En mathématiques : convergence dans la suite de Fibonacci, optimisation géométrique

Mais aucune source ne mentionne explicitement que atteindre 1/φ dans une opération rend la marche inverse impossible ou que cela constitue un piège numérique.